1.3. The Evolution of Learning Systems
Before we tackle advanced concepts in machine learning and artificial intelligence, it is also important to take a step back and understand how learning systems evolved through time.
This lesson is not about the history of artificial intelligence. Instead, it is about how modern learning systems developed from rudimentary statistics and mathematics.
Like in any biological or geological event, we will divide the evolution of learning systems into three eras: Statistical Models Era, Machine Learning Era, and the Deep Learning Era.
Understanding these shifts in thinking is crucial for us to grasp how modern machine learning systems reason, generalize, and adapt.
Statistical Models Era (1950s–1980s)
The Statistical Models Era laid the groundwork for machine learning by framing learning as a problem of inference and optimization under uncertainty. Before machine learning and AI was even a structured field of study, researchers have been extracting structure from data using statistical principles.
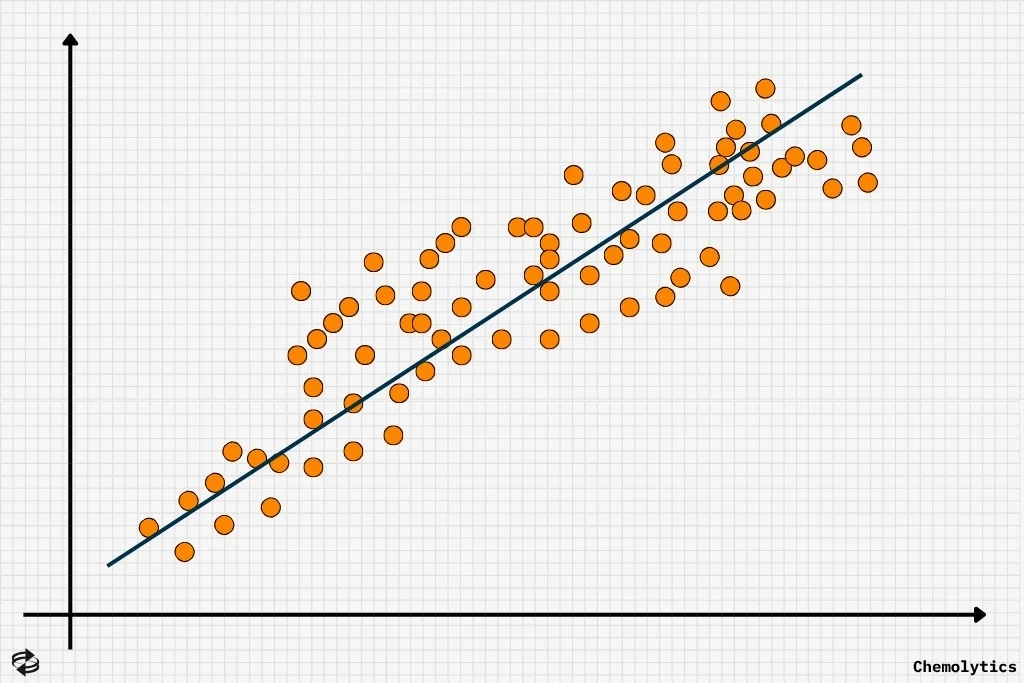
One of the most influential techniques during this time was linear regression. This technique models the relationship between a dependent variable and one or more independent variables. It does so by fitting a line that minimizes the error between predicted and actual values.
While linear regression traces its roots with Isaac Newton’s calculations on equinoxes around 1700, it was established in the 20th century through the method of ordinary least squares (OLS).
OLS served as the groundwork tool for statistical prediction and still remains as a baseline model in supervised learning tasks. In fact, it is still being used today to interpolate unknown data from known independent and dependent variables. For example, OLS is still being used to determine the concentration of an unknown substance using concentration vs absorbance plots.
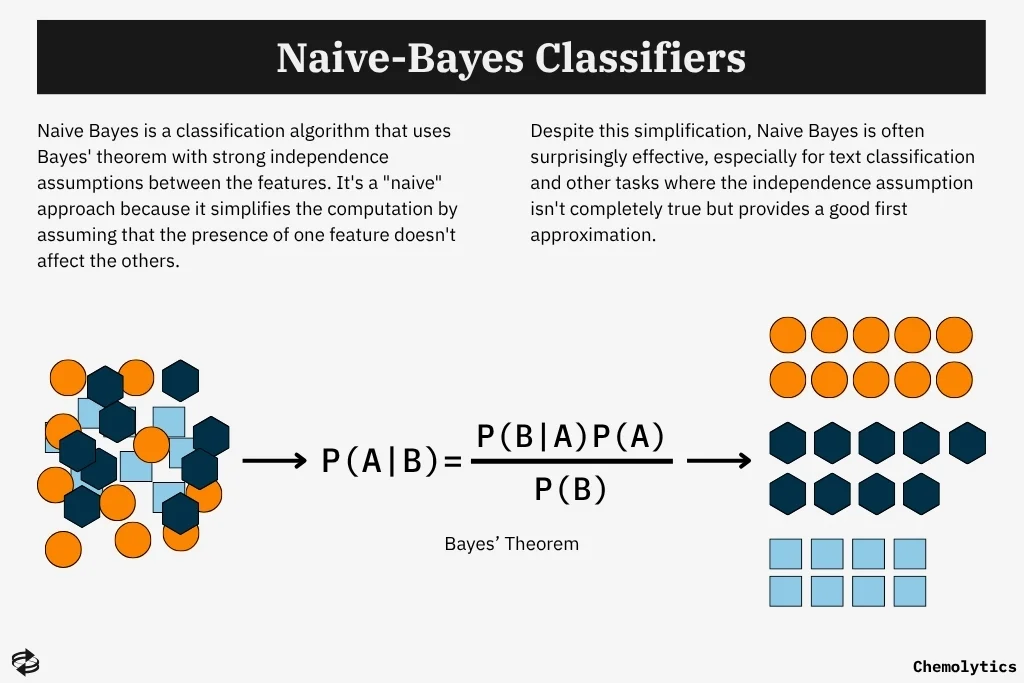
All the while, Bayesian learning and the earliest forms of probabilistic inference gained momentum. These approaches treated learning as an update of old beliefs when new evidence was given, formalized through Bayes’ theorem.
Models like Naïve-Bayes and Gaussian classifiers also emerged. These models assumed a known data distribution and prioritized computational simplicity, offering early successes in pattern recognition and text classification.
Another major development during the Statistical Models era was decision theory. Decision theory approached learning as an optimization problem, where expected loss or error in decision-making is minimized.
This period also saw the birth of the perceptron in 1958. The perceptron is human’s earliest attempts in simulating the learning processes using a neural structure. Although initially limited to linearly separable problems, the perceptron introduced key ides in iterative optimization and supervised learning.
During the Statistical Models era, the most dominant view of learning was constructing models that generalize from labeled examples. Learning systems operated with strong assumptions about the data’s statistical distribution and were highly constrained by computational resources and small datasets. As such, the work was primarily situated in statistics, signal processing, and information theory rather than in a unified field of machine learning.
In sum, this era established critical statistical principles and algorithms that would become the backbone of more flexible and scalable learning systems in later decades. It was a time of theoretical precision but practical limitations, shaping the early contours of data-driven modeling.
Machine Learning Era (1990s–2010s)
The Machine Learning era marked the transition from theoretical formulations to practical, scalable algorithms capable of uncovering patterns in real-world data. With improved computational power, better datasets, and more advances in statistical theory, this period saw machine learning mature into a distinct discipline focused on generalizing rather than memorizing.
One of the most impactful developments during this era was the emergence of algorithms such as support vector machines (SVM), decision trees, and ensemble methods. These algorithms prioritized performance on unseen data, introducing formal strategies to balance model complexity and predictive accuracy.
The field was also shaped by a strong theoretical foundation. The PAC (Probably Approximately Correct) Learning Framework, introduced by Leslie Valiant, provided a formal basis to assess whether a hypothesis class could generalize well given finite samples. This era saw intense research into VC dimension, model capacity, and generalization bounds, forming the statistical backbone of learning theory.

To address overfitting and high-dimensional problems, regularization techniques like Lasso (L1) and Ridge (L2) regression were introduced. These methods imposed constraints on model complexity, enabling learning from underdetermined systems and noisy datasets.
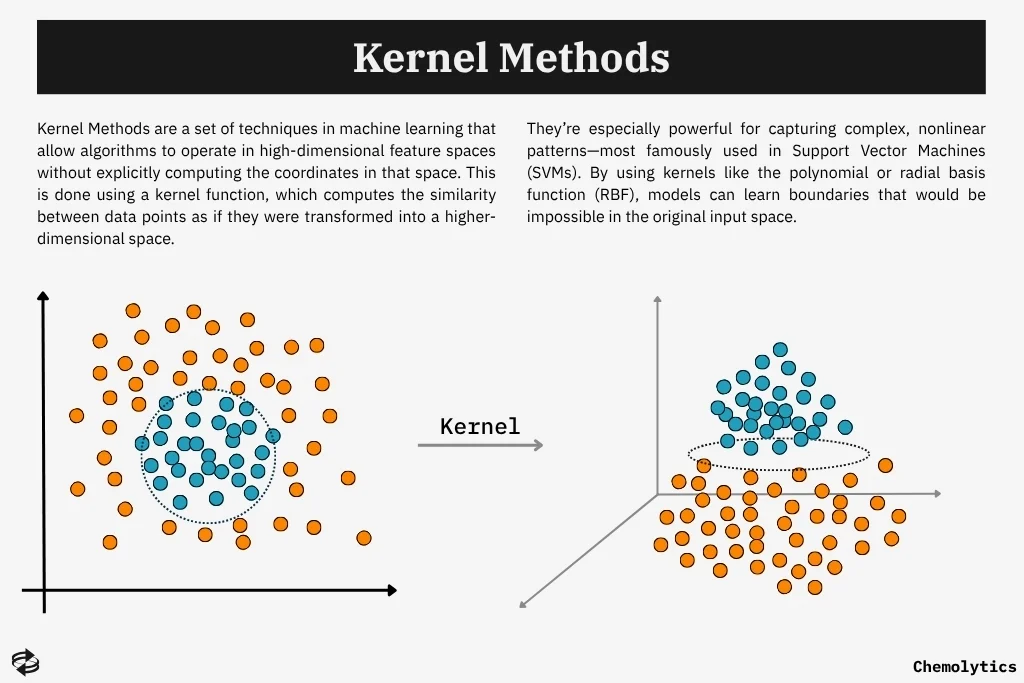
Another critical advancement was the introduction of kernel methods. Kernel methods extended linear algorithms to handle non-linear relationships in high-dimensional feature spaces. The kernel trick also allowed SVM and other supervised learning models to operate in implicitly transformed spaces. This opened up new possibilities in computer vision and bioinformatics.
Simultaneously, unsupervised learning gained traction, with algorithms such as k-means clustering, Principal Component Analysis (PCA), and Expectation-Maximization (EM) being applied to structure discovery, dimensionality reduction, and generative modeling.
Semi-supervised learning also emerged as a bridge between labeled and unlabeled data scenarios, offering efficiency in data-scarce settings.
Practitioners increasingly embraced empirical risk minimization over purely theoretical assumptions. They relied on cross-validation for model selection and performance evaluation.
This practical mindset drove the development of benchmark datasets (e.g., UCI ML Repository) and the rise of open-source toolkits like Weka, scikit-learn, and libSVM, which democratized access to machine learning workflows.
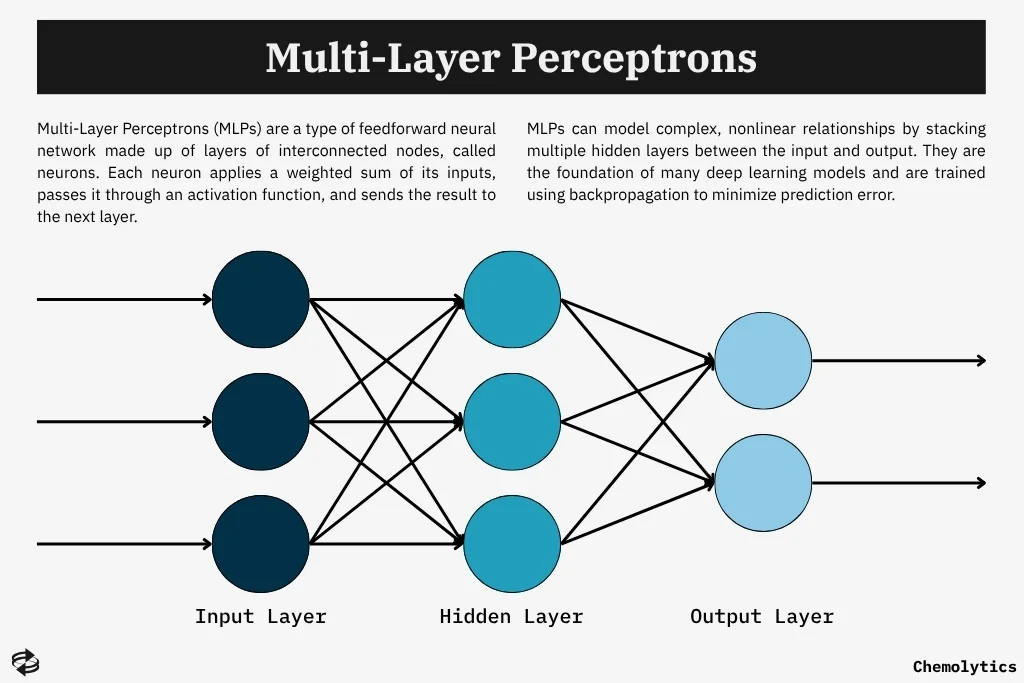
Toward the late 2000s, neural networks, especially multilayer perceptrons, resurfaced with modest success, though their potential remained constrained by limited data and computational power. Nonetheless, the groundwork laid in this era set the stage for the deep learning revolution that followed.
Overall, the Machine Learning Era was defined by a shift from symbolic logic to empirical, data-driven modeling, advancing the field from theoretical elegance to robust practical impact.
Deep Learning Era (2010s–Present)
The Deep Learning Era transformed machine learning from a domain of handcrafted features and task-specific models into a field dominated by end-to-end architectures capable of learning representations directly from raw data. Powered by advances in hardware, data availability, and algorithmic innovation, this period redefined the boundaries of what learning systems could achieve.
The breakthrough moment came in 2012, when AlexNet, a deep convolutional neural network, dramatically outperformed traditional models in the ImageNet competition. This success was driven by the use of GPUs for training, deeper architectures, and large-scale datasets, ushering in the age of deep neural networks for vision, speech, and language.
Central to this era is the principle of representation learning. Rather than manually engineering features, models learned multi-level abstractions automatically.
Convolutional Neural Networks (CNNs) revolutionized image processing by capturing spatial hierarchies. Recurrent Neural Networks (RNNs) and later Long Short-Term Memory (LSTM) units extended this capacity to sequential data like speech and text.
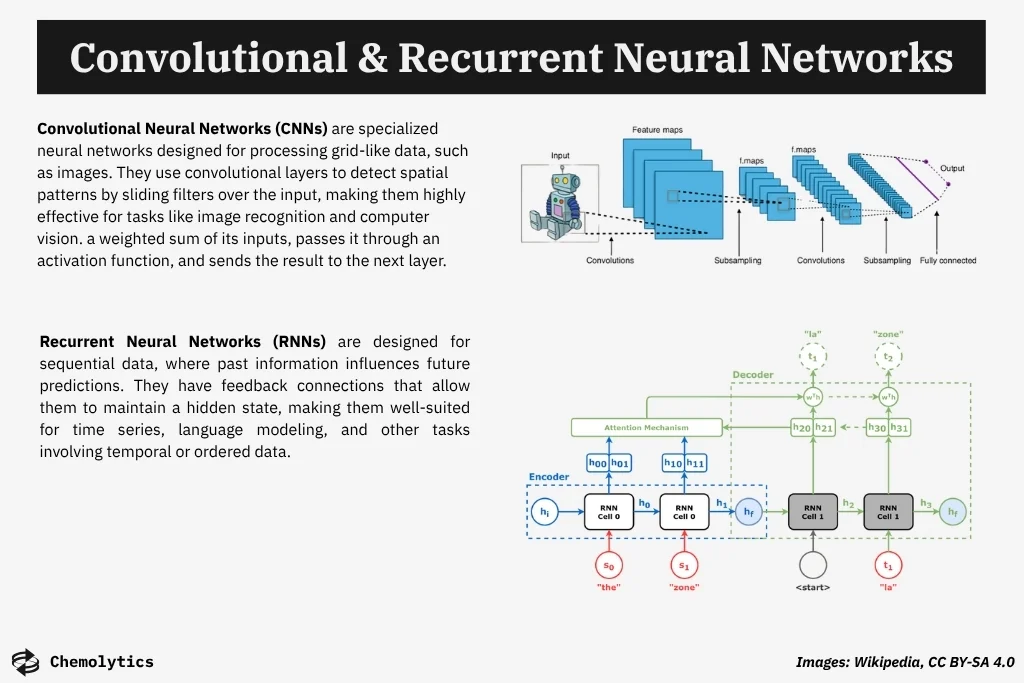
The introduction of transformer architectures (2017) radically changed natural language processing by enabling parallelizable attention-based learning, setting the stage for large language models.
These model architectures would not be possible without the advances in optimization techniques such as Adam, RMSprop, and gradient clipping. On top of that, the rise of automatic differentiation frameworks like TensorFlow and PyTorch abstracted away the complexity of model definition and backpropagation.
A defining shift of this era is the movement toward pre-trained general-purpose models. Systems like BERT and GPT are trained on massive corpora and fine-tuned for downstream tasks, making it feasible to achieve state-of-the-art performance with minimal labeled data.
This gave rise to the era of foundation models—large, reusable neural networks serving as the base for a wide variety of applications.
The open-source machine learning ecosystem also exploded, with tools like Hugging Face Transformers, Lightning, and ONNX enabling rapid development, deployment, and sharing of models across industries and research domains.
At the same time, the rise of model scale and complexity spurred efforts in data-centric AI, shifting focus from architecture to dataset quality, and interpretability research, aiming to make these opaque systems more understandable and trustworthy.
In summary, the Deep Learning Era represents a paradigm shift: learning systems evolved from isolated models built around features to highly scalable, self-improving architectures capable of generalized reasoning across tasks and modalities. It is the era of automation at scale, and the foundation of the current frontier in artificial intelligence.
Why This Evolution Matters
Understanding the historical evolution of learning systems is essential for developing a critical perspective on modern machine learning. Each era reflects the tools, constraints, and philosophical assumptions of its time.
By tracing how learning models evolved from statistical inference to pattern recognition to deep representation learning, practitioners gain a deeper appreciation for the design choices underlying today’s technologies.
As AI moves closer to general-purpose reasoning systems, the convergence of symbolic reasoning with neural architectures is poised to redefine what learning systems can do. The emerging neural-symbolic synthesis seeks to combine the logical structure of classical AI with the adaptive power of deep learning. This frontier reflects a return to earlier aspirations—interpretable, compositional, and generalizable intelligence—now approached with modern tools and data.
In essence, knowing where machine learning came from is key to shaping where it’s going. This evolution is a roadmap for innovation, accountability, and the responsible development of intelligent systems.

